前回の予告通りパチンコ・スロットの計算に使えそうな関数を紹介したいと思います。
まずは「BINOMIDIST」関数です。新しいバージョンのエクセルではBINOM.DISTだったりするようですが、オープンオフィスでの書式になっています。
ただし入力内容はほとんど変わらない、できるだけ細かく説明したいと思うので対応できると思います・・・
BINOMDIST関数
この関数は二項分布の確率を求める事ができます。
簡単に説明すると条件を設定してそれが成功するか失敗するかの確率を求める事が出来ます。
パチンコ・スロットの確率計算にとても相性の良い関数です。。。
入力書式は「 BINOMDIST(成功回数; 試行回数; 確率; 関数形式) 」です。
順に確認してみたいと思います。
成功回数:試行が成功する回数。大当り回数とでも置き換えるとイメージしやすいと思います
試行回数:試行する回数です()。これも置き換えると回転数です。何回転させた時の結果が知りたいか?です
確率:1回の試行が成功する確率。大当り確率、小役確率とかです。
関数形式:2パターンあり「0」で単一事象の確率、「1」で累積確率を求める事が出来ます。
0の場合x回回した時にちょうどy回大当りする確率
1の場合x回回した時にy回以下の大当り回数の確率を求める事が出来ます。
これで一通り説明出来たと思うので実際に数値を入力してみたいと思います。
まずは簡単な例でコイントスを6回した場合に3回表が出る確率を計算してみたいと思います。
入力する数値は成功回数:3、試行回数:6、確率:0.5、関数形式:0を入力します。
「 BINOMDDIST(3;6;0.5;0) 」
大体いくつくらいになるか予想してみてください。
答えは・・・
・・
・
=0.3125 ≒31%となります
予想通りでしたでしょうか?
なんとなく少ない(50%ではないの?)と思った方も多いかもしれません。
今回の計算は関数形式0の単一事象、ちょうど3回出る確率を計算しているからです。
二分の一の確率なので3回出る確率が1番高いのですが、成功回数を2回にして計算してみて欲しいと思います。
すると答えは約23%になると思います。
この関係をグラフにしてみると
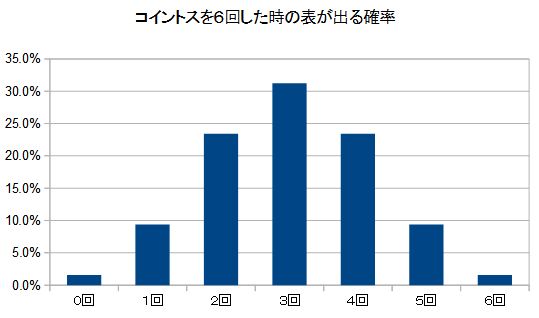
2回~4回を合計すると約78%になります。
ピッタリ3回という事はないけれど大体2~4回でる可能性が高いと言えると思います。
次に条件設定は上と同じにして関数形式のみ「1」にします。
「 BINOMDDIST(3;6;0.5;1) 」
答えは65.6%となります。
この値は表の回数が3回以下になる確率です。
関数形式「0」の0回~3回を合計しても同様の数値になっていると思います。
言い換えると確率分母以上引ける引き強の方は1-0.656=0.344。約34%の方が引き強という事です。
次にパチンコ・スロットでの使い所をイメージしやすいように実機の数値を使って計算してみたいと思います。
例題として「CRフィーバー戦姫絶唱シンフォギア」の大当り確率1/199.8を使用して考えてみます。
皆さんはどう考えているかわかりませんが、いつもオスイチ(1k)で当てたいと考えているかもしれません。
ただ中々そんな事は無いと思います。
では実際にオスイチで当たる可能性は何%であるのか少し計算してみたいと思います。
1/199.8の確率の機種を打って1k(20回転)で当たるという事は、1kで当たらない確率を除いたものと考えます。
「 BINOMDDIST(0;20;1/199.8;0) 」
※今回の場合成功回数0回の為関数形式0と1どちらを使用しても同じ値になります。
答えは0.9045・・・
90%以上は1kでは当りません。求めたい値は1kで当たる確率なので・・・
1-0.9045=0.0955
という事で10%弱は1kで当たる事になります。
オスイチで当たらなければ続けて打たないと考える人もいるかもしれませんが、せめて確率分母内(約1/200)で当てたいと思ってそのまま続行した場合どうなるか?
「 BINOMDDIST(0;200;1/199.8;0) 」
=0.36658・・・
同様に当たる確率は1-0.3666=0.6334
約63%が確率分母内で当りが引けます。
この割合はミドルスペックの1/320でも甘デジの1/100でも大体同じ同じで確率分母まで回すと約2/3で大当りが引けますが、約1/3で大当りが引けないです。
ここまできたら当たるまでと考えて打っているけど中々当たらない。。。
1000回はまる確率を計算してみます。
「 BINOMDDIST(0;1000;1/199.8;0) 」
=0.00662・・・
約0.7%です。151回に1回くらいは1000回まわしても当たらない事になります。
多いと考えるか少ないと考えるかは個人の判断におまかせしますが、何台も設置している大型店なら1000ハマリしているシンフォギアを毎日見かける事もおかしくないと思います。
色々な理由が重なってあのお店は怪しいと考えるかもしれませんが、これくらいは起きる可能性があるという事は理解してください。


